SETS
Introduction
Definition
It's a collection. First we specify a common property among "things" (this word will be defined later) and then we gather up all the "things" that have this common propertyFor example, the items you wear: shoes, socks, hat, shirt, pants, and so on. I'm sure you could come up with at least a hundred. This is known as a set
Or another example is types of fingers. This set includes index, middle, ring, and pinky.
|
Notation
There is a fairly simple notation for sets. We simply list each element (or "member") separated by a comma, and then put some curly brackets around the whole thing:The curly brackets { } are sometimes called "set brackets" or "braces".
This is the notation for the two previous examples:
{socks, shoes, watches, shirts, ...}
{index, middle, ring, pinky}
Notice how the first example has the "..." (three dots together){index, middle, ring, pinky}
The three dots ... are called an ellipsis, and mean "continue on".
Example
The set of letters:
{a, b, c, ..., x, y, z}
In this case it is a finite set (there are only 26 letters, right?)
Numerical Sets
So what does this have to do with mathematics? When we define a set, all we have to specify is a common characteristic. Who says we can't do so with numbers?
Set of even numbers: {..., -4, -2, 0, 2, 4, ...}
Set of odd numbers: {..., -3, -1, 1, 3, ...}
Set of prime numbers: {2, 3, 5, 7, 11, 13, 17, ...}
Positive multiples of 3 that are less than 10: {3, 6, 9}
And the list goes on. We can come up with all different types of setsSet of odd numbers: {..., -3, -1, 1, 3, ...}
Set of prime numbers: {2, 3, 5, 7, 11, 13, 17, ...}
Positive multiples of 3 that are less than 10: {3, 6, 9}
There can also be sets of numbers that have no common property, they are just defined that way.
For example:
{2, 3, 6, 828, 3839, 8827}
{4, 5, 6, 10, 21}
{2, 949, 48282, 42882959, 119484203}
Are all sets that I just randomly banged on my keyboard to produce{4, 5, 6, 10, 21}
{2, 949, 48282, 42882959, 119484203}
Universal Set
At the start we used the word "things" in quotes. We call this the universal set. It's a set that contains everything. Well, not exactly everything. Everything that is relevant to our questionThen our sets included integers. The universal set for that would be all the integers. In fact, when doing Number Theory, this is almost always what the universal set is, as Number Theory is simply the study of integers
However in Calculus (also known as real analysis), the universal set is almost always the real numbers. And in complex analysis, you guessed it, the universal set is the complex numbers
Equality
Two sets are equal if they have precisely the same members. Now, at first glance they may not seem equal, so we may have to examine them closely!Example
Are A and B equal where:- A is the set whose members are the first four positive whole numbers
- B = {4, 2, 1, 3}
And the equals sign (=) is used to show equality, so we write:
A = B
Subsets
When we define a set, if we take pieces of that set, we can form what is called a subset.So for example, we have the set {1, 2, 3, 4, 5}. A subset of this is {1, 2, 3}. Another subset is {3, 4} or even another, {1}. However, {1, 6} is not a subset, since it contains an element (6) which is not in the parent set. In general:
A is a subset of B if and only if every element of A is in B.
Example
Is A a subset of B, where A = {1, 3, 4} and B = {1, 4, 3, 2}?1 is in A, and 1 is in B as well. So far so good.
3 is in A and 3 is also in B.
4 is in A, and 4 is in B.
That's all the elements of A, and every single one is in B, so we're done.
Yes, A is a subset of B
Note that 2 is in B, but 2 is not in A. But remember, that doesn't matter, we only look at the elements in A.
Let A be all multiples of 4 and B be all multiples of 2. Is A a subset of B? And is B a subset of A?
The sets are:
- A = {..., -8, -4, 0, 4, 8, ...}
- B = {..., -8, -6, -4, -2, 0, 2, 4, 6, 8, ...}
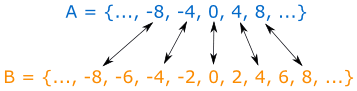
A is a subset of B, but B is not a subset of A
Why Are Sets Important?
Sets are the fundamental property of mathematics. Now as a word of warning, sets, by themselves, seem pretty pointless. But it's only when we apply sets in different situations do they become the powerful building block of mathematics that they are
Math can get amazingly complicated quite fast. Graph Theory, Abstract Algebra, Real Analysis, Complex Analysis, Linear Algebra, Number Theory, and the list goes on. But there is one thing that all of these share in common: Sets.
References:



